Dites adieu aux tracas de transformer les matrices manuellement avec la calculatrice RREF révolutionnaire! Conçu spécialement pour les mathématiciens, cette application convertit sans effort toute matrice en sa forme d'échelon réduite. Dites bonjour à l'algèbre linéaire simplifiée! Ne serez plus jamais découragé par des calculs complexes - cet outil ingénieux est là pour sauver la journée. Gardez le feu de votre curiosité mathématique qui brûle lorsque vous débloquez la solution aux problèmes les plus perplexes. Dites bonjour à la facilité et à l'efficacité, et offrez des adieux à la frustration. Ne manquez pas l'opportunité de révolutionner votre voyage mathématique - téléchargez l'application aujourd'hui!
Caractéristiques de la calculatrice RREF:
a) Transformation de la matrice pratique : l'application offre un moyen pratique de transformer n'importe quelle matrice en forme d'échelon en ligne réduite. Cette caractéristique est particulièrement bénéfique pour les mathématiciens et les étudiants qui étudient l'algèbre linéaire car il simplifie les calculs complexes.
b) Convient à tous les niveaux : que vous soyez un débutant ou un mathématicien expérimenté, cette application s'adresse à tous les niveaux de compétence. Il peut être tout aussi utile pour les étudiants qui apprennent les bases des matrices et des professionnels travaillant sur des problèmes mathématiques avancés.
c) Outil de gain de temps : en automatisant le processus de transformation des matrices, l'application permet aux utilisateurs beaucoup de temps et d'efforts. Plus de calculs manuels ou d'étapes fastidieux - entrez simplement dans la matrice, et l'application fournira instantanément le formulaire d'échelon réduit.
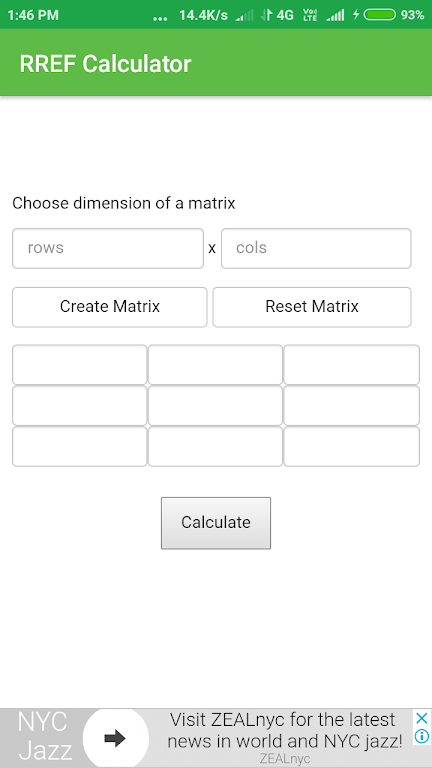
d) Interface conviviale : l'application possède une interface conviviale, ce qui facilite la navigation et le fonctionnement même pour ceux qui ne sont pas avertis en technologie. Il offre une expérience utilisateur sans couture et sans tracas, garantissant que les utilisateurs peuvent se concentrer sur leurs problèmes mathématiques sans aucune distraction.
Conseils pour les utilisateurs:
A) Comprendre la notation de la matrice : Avant d'utiliser l'application, il est essentiel de vous familiariser avec la notation de la matrice et de comprendre comment entrer correctement les matrices. Ces connaissances garantiront des résultats précis et une expérience fluide avec l'application.
b) Entrée à double vérification : pour éviter toute erreur ou erreur de calcul, vérifiez toujours la matrice d'entrée avant de calculer la forme d'échelon de ligne réduite. Même les petites erreurs peuvent entraîner des sorties incorrectes, donc prendre quelques secondes supplémentaires pour vérifier les données peut vous faire gagner du temps à long terme.
c) Explorer les fonctionnalités avancées : Bien que l'application excelle dans la transformation des matrices, il peut offrir des fonctionnalités supplémentaires pour améliorer votre expérience mathématique. Prenez le temps d'explorer les paramètres et les options de l'application pour découvrir tous les joyaux cachés qui peuvent optimiser davantage votre utilisation.
d) Utiliser des matrices enregistrées : de nombreux calculatrices RREF permettent aux utilisateurs d'économiser ou de stocker des matrices pour une utilisation future. Profitez de cette fonctionnalité pour créer une bibliothèque de matrices fréquemment utilisées, ce qui vous fait gagner du temps en les entrant manuellement à plusieurs reprises.
Conclusion:
La calculatrice RREF est un outil puissant qui simplifie les transformations matricielles et élimine les frustrations souvent associées aux calculs manuels. Avec ses fonctionnalités pratiques, son interface conviviale et son aptitude à tous les niveaux de compétence, cette application est un incontournable pour les mathématiciens, les étudiants et les professionnels. En gardant le temps et les efforts des utilisateurs, l'application maintient l'intérêt pour les mathématiques en vie et aide les utilisateurs à résoudre des problèmes complexes sans effort. Téléchargez l'application maintenant et autonomisez-vous les capacités de transformation de la matrice efficace de l'application.