これらの秘密のコードを使用して、モバイル ロイヤルで信じられないほどの宝物をアンロックしましょう! これらのコードは宝箱への鍵のようなもので、貴重なリソースと王国を征服するためのブーストを即座に与えます。 木材や宝石などの必須資源にアクセスできるようになり、資源収集の長い待ち時間がなくなりました。
部隊の訓練と建設を加速したいですか?これらのコードは Speed Up トークンを提供し、待ち時間を大幅に短縮します。 延々と待つ必要はもうありません – 1 つのコードで大幅に有利なスタートを切ることができます。
アクティブな Mobile Royale 引き換えコード:
MR24BS: 報酬には、食料 200,000,000、木材 50,000,000、石 40,000,000、ゴールド 20,000,000、VIP ポイント 1,000、スピードアップ アイテム 600 分、24 時間シールド 1 個、および 500 x が含まれます。 10分間のスピードアップアイテム。
Mobile Royale でコードを引き換える方法:
- ゲーム内プレーヤーのアバターをタップします。
- 画面の下部にある「その他」タブを選択します。
- 「Exchange コード」設定を見つけます。
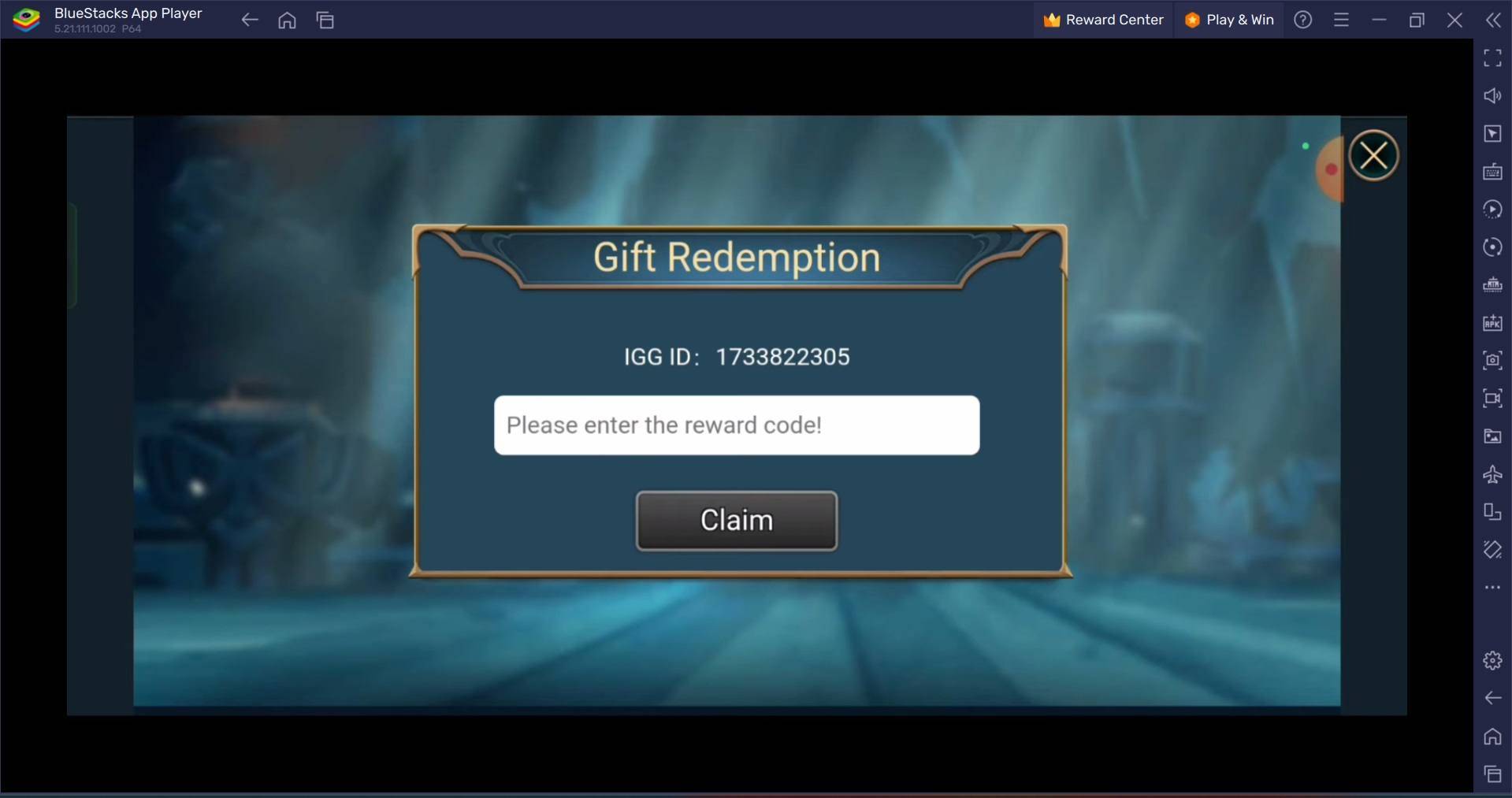
- コードを入力して特典を受け取ります。
コードが機能しない理由:
- 有効期限: 一部のコードは、有効期限が明記されていない場合でも有効期限が切れます。
- 大文字と小文字の区別: コードでは大文字と小文字が区別されます。大文字と小文字が正確に区別されるようにします。 最良の結果を得るには、このリストから直接コピーして貼り付けてください。
- 引き換え制限: コードは通常、アカウントごとに 1 回のみ使用できます。
- 使用制限: 一部のコードには引き換え回数が制限されています。
- 地域制限: コードは地域固有である場合があります。
最適なゲーム体験を得るには、BlueStacks を使用して PC でモバイル ロイヤルをプレイし、大きな画面でキーボードとマウスのコントロールでスムーズなゲームプレイをお楽しみください。















