Tauchen Sie in die aufregende Welt der "Zusammenführen von Zahlen auf den Bällen und rennen Sie um 2048", ein dynamisches Ballspiel, das Ihre Fähigkeiten und Strategie in Frage stellen soll. Das Ziel ist einfach und doch faszinierend: Leiten Sie die Bälle mit Ihrem Finger und verschmelzen sie, um die Zahlen auf ihnen zu erhöhen, mit dem ultimativen Ziel, 2048 zu erreichen.
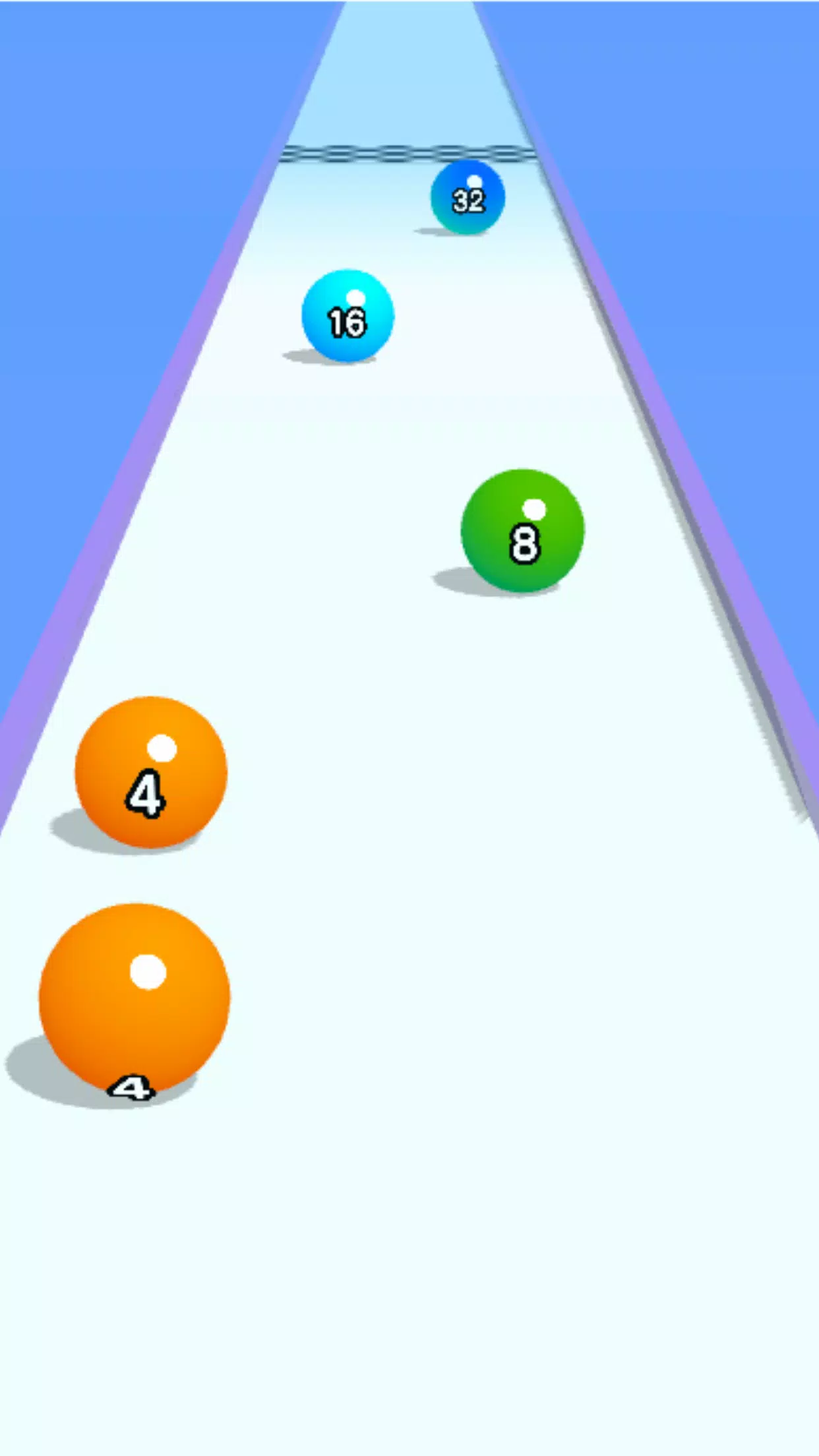
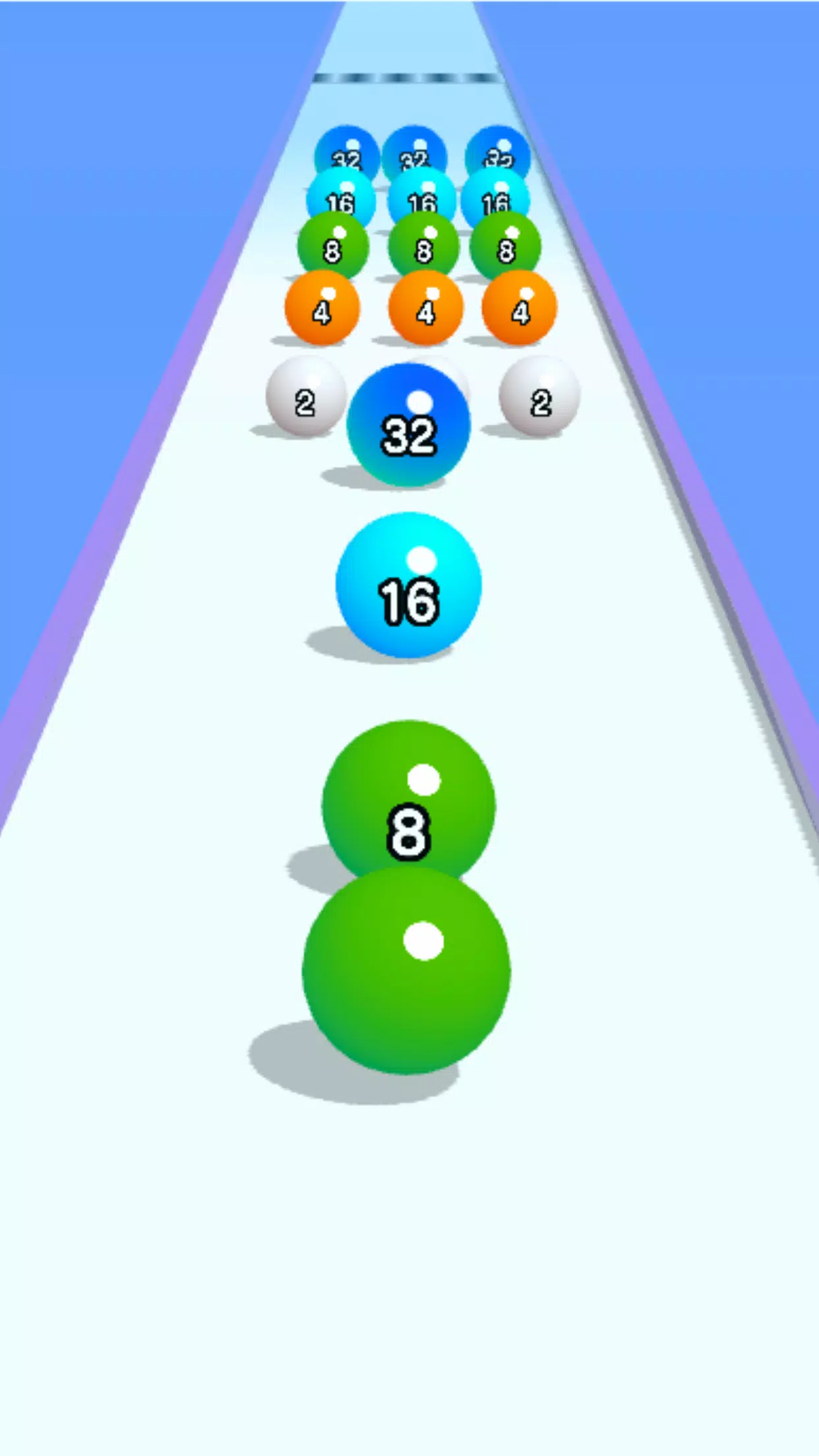
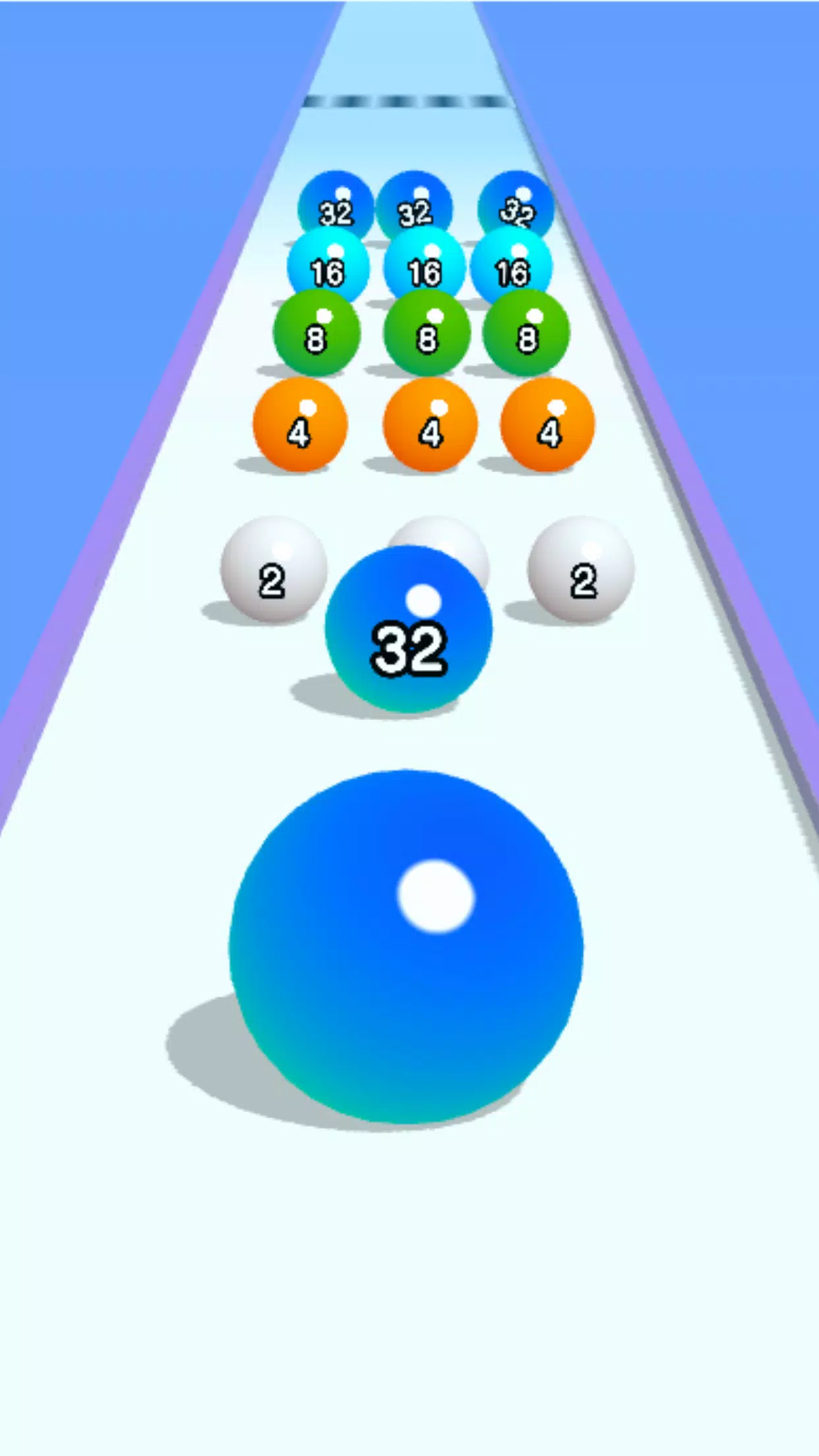
In diesem Spiel beginnen Sie mit den Bällen, die 2 nummeriert sind. Wenn Sie einen Ball gekonnt manövrieren, um mit einem anderen von dem gleichen Wert zusammenzuarbeiten, kombinieren sie die Anzahl, verdoppelt die Anzahl und ändern sich die Farbe, wodurch ein visuell atemberaubendes Fortschreiten erzeugt wird. Während Sie Fortschritte machen, folgen die Zahlen auf den Bällen der Sequenz 2-4-8-16-32-64-128-256-512-1024-2048. Mit jeder erfolgreichen Zusammenführung wird der Ball größer und die Herausforderung verstärkt sich.
Während das Spiel für Kinder zugänglich genug ist, ist das Erreichen des begehrten 2048 eine beeindruckende Aufgabe, die Präzision und Strategie erfordert. Navigieren Sie den Kurs sorgfältig und stellen Sie sicher, dass Ihr Ball nicht abfällt oder mit Hindernissen kollidiert, wodurch Sie Ihren Fortschritt zurücksetzen oder die Anzahl auf Ihrem Ball reduzieren können. Der Nervenkitzel der Verschmelzung von Bällen zur Bildung eines Regenbogen-farbigen 2048-Balls verleiht Ihrem Gameplay eine zusätzliche Aufregung.
Regeln Beschreibung:
Wischen Sie, um die Bewegung Ihres Balls über die Strecke zu steuern. Wenn Ihr Ball mit der gleichen Anzahl auf einen anderen trifft, verschmelzen sie und erhöhen den Wert. Seien Sie jedoch vorsichtig mit den Rändern und Dornen des Kurses; Wenn Sie abfallen, beginnen Sie von vorne, und wenn Sie einen Dorn treffen, verringert es die Anzahl Ihres Balls.
Die Belohnungen beim Tor eskalieren mit der Anzahl Ihres Balls und machen jeden erfolgreichen Zusammenschluss nicht nur einen Schritt in Richtung 2048, sondern auch in Richtung größerer Belohnungen. Können Sie die Kunst des Zusammenführens beherrschen und den Regenbogen-Farben 2048-Ball erreichen?
